Números racionales: clave para aproximar reales

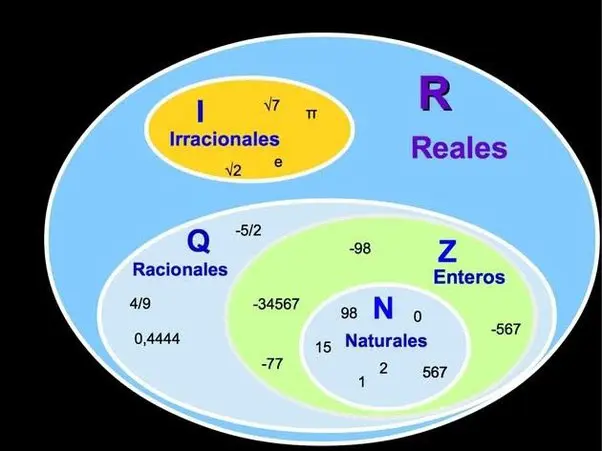
En el vasto universo matemático, los números juegan un papel fundamental. Entre ellos, los números reales y los números racionales ocupan un lugar destacado. Los números reales abarcan todos los números que podemos imaginar, incluyendo los enteros, los decimales, los irracionales y los complejos. Por otro lado, los números racionales son aquellos que pueden expresarse como una fracción de dos enteros.

Una pregunta que surge naturalmente es: ¿Qué relación existe entre estos dos conjuntos numéricos? En este artículo, exploraremos la profunda conexión entre los números reales y los racionales, un hecho sorprendente: para todo número real existe una sucesión de números racionales que se aproximan a él.

El concepto de número racional

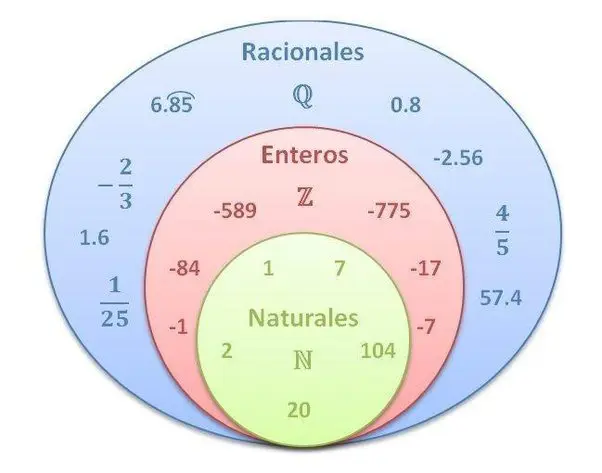
Un número racional es aquel que puede representarse como una fracción de dos enteros, donde el denominador no es cero. Por ejemplo, 1/2, 3/4, -5/7 y 2 son todos números racionales. La característica distintiva de un número racional es que su representación decimal es finita o periódica.

Por ejemplo, 1/2 se representa como 0.5, que es una representación decimal finita. 3/4 se representa como 0.75, también finita. Y 1/3 se representa como 0.33., con una secuencia de 3 que se repite infinitamente, lo que indica una representación decimal periódica.

La importancia de los números racionales

Los números racionales son esenciales en diversas áreas de la matemática y las ciencias. Se utilizan en operaciones aritméticas básicas como la suma, la resta, la multiplicación y la división. También son fundamentales en la teoría de números, la geometría y el análisis.

En la vida cotidiana, los números racionales se utilizan para representar cantidades como fracciones de un todo, porcentajes y medidas. Por ejemplo, si queremos expresar la mitad de una pizza, podemos usar la fracción 1/O si queremos calcular el 20% de un precio, podemos usar la fracción 20/100.

El teorema fundamental: Para todo número real existe una sucesión de racionales

Este teorema establece que dado un número real cualquiera, podemos encontrar una secuencia infinita de números racionales que se acerquen cada vez más a él. En otras palabras, podemos aproximar cualquier número real con la precisión que deseemos utilizando números racionales.

Este hecho tiene implicaciones profundas en el estudio de los números reales y en la construcción de sistemas numéricos. Permite, por ejemplo, definir operaciones como la suma, la resta, la multiplicación y la división en el conjunto de los números reales a partir de las mismas operaciones en el conjunto de los números racionales.

Ejemplo ilustrativo

Consideremos el número real π (pi), que es un número irracional. Sabemos que π es aproximadamente 1415Podemos construir una sucesión de números racionales que se acerquen a π de la siguiente manera:

• 3
• 1
• 14
• 141
• 1415
• 14159

Cada término de esta sucesión es un número racional y se acerca progresivamente a π. A medida que avanzamos en la sucesión, la diferencia entre el término y π se reduce.

Demostración del teorema

Para demostrar este teorema, podemos utilizar el concepto de intervalos encajados. Un intervalo encajado es una secuencia de intervalos cerrados que se van reduciendo en tamaño y tienen un punto en común.

Dada un número real x, podemos construir una sucesión de intervalos encajados que contengan a x. Cada intervalo estará formado por dos números racionales.

Para el primer intervalo, podemos tomar el entero más pequeño que x y el entero más grande que x. Para el segundo intervalo, podemos tomar el punto medio del primer intervalo y otro punto racional que esté a una distancia de 1/2 del punto medio. Podemos continuar de esta manera, dividiendo cada intervalo en dos partes iguales y tomando dos puntos racionales dentro de cada parte.

Al final, obtendremos una sucesión de intervalos encajados que contienen a x. El punto en común de todos estos intervalos será x. Como cada intervalo está formado por dos números racionales, tendremos una sucesión de números racionales que convergen a x.

Aplicaciones del teorema

El teorema para todo número real existe una sucesión de racionales tiene aplicaciones en diversas áreas de la matemática y las ciencias. Algunas de ellas son:

• Aproximación de funciones: El teorema permite aproximar funciones reales con funciones racionales. Esto es útil en el análisis numérico y en la construcción de modelos matemáticos.
• Cálculo numérico: Muchos métodos numéricos para resolver ecuaciones diferenciales y problemas de optimización se basan en la aproximación de funciones reales con funciones racionales.
• Teoría de la medida: El teorema se utiliza en la teoría de la medida para construir medidas en el conjunto de los números reales.
• Probabilidad: En probabilidad, el teorema se utiliza para construir variables aleatorias continuas a partir de variables aleatorias discretas.

¿Cómo se puede encontrar una sucesión de números racionales que se aproximen a un número real dado?

Para encontrar una sucesión de números racionales que se aproximen a un número real dado, podemos utilizar el método de los intervalos encajados. Este método consiste en construir una secuencia de intervalos cerrados que se van reduciendo en tamaño y tienen un punto en común. Cada intervalo estará formado por dos números racionales.

¿Es posible encontrar una sucesión de números racionales que converja a un número irracional?

Sí, es posible encontrar una sucesión de números racionales que converja a un número irracional. De hecho, el teorema para todo número real existe una sucesión de racionales se aplica a todos los números reales, incluidos los irracionales.

¿Qué significa que una sucesión de números racionales converja a un número real?

Que una sucesión de números racionales converja a un número real significa que a medida que avanzamos en la sucesión, la diferencia entre el término de la sucesión y el número real se reduce. En otras palabras, los términos de la sucesión se acercan cada vez más al número real.

¿Qué relación tiene el teorema para todo número real existe una sucesión de racionales con la densidad de los números racionales?

El teorema para todo número real existe una sucesión de racionales está estrechamente relacionado con la densidad de los números racionales. La densidad de los números racionales significa que entre dos números racionales cualesquiera, siempre existe otro número racional. Este hecho implica que los números racionales están repartidos de manera densa en la recta real.

¿Cómo se puede utilizar el teorema para todo número real existe una sucesión de racionales en la vida real?

El teorema para todo número real existe una sucesión de racionales tiene aplicaciones en diversas áreas de la vida real, como la ingeniería, la física, la economía y la informática. Por ejemplo, se utiliza para aproximar valores de constantes físicas, para construir modelos matemáticos de fenómenos naturales y para diseñar algoritmos de aprendizaje automático.

El teorema para todo número real existe una sucesión de racionales es un resultado fundamental en la matemática que establece una profunda conexión entre los números reales y los racionales. Este teorema tiene implicaciones importantes en el estudio de los números reales y en la construcción de sistemas numéricos.

Al comprender este teorema, podemos apreciar la riqueza y la complejidad del sistema numérico real. Además, nos proporciona una herramienta poderosa para aproximar números reales con números racionales, lo que tiene aplicaciones en diversas áreas de la ciencia y la tecnología.

Si quieres conocer otros artículos parecidos a Números racionales: clave para aproximar reales puedes visitar la categoría Historias reales.